Mais de quoi parlons-nous au nom d'Évariste Galois ?

Avant de plonger dans le terrier du lapin cryptographique, voyons ce que sont réellement les corps de Galois. Nommés d'après le jeune mathématicien français Évariste Galois (qui, petite anecdote, est mort en duel à 20 ans - une sortie spectaculaire), ces corps sont des ensembles finis d'éléments avec des propriétés algébriques spéciales.

En termes plus simples, imaginez un terrain de jeu où les nombres suivent des règles très spécifiques. Ces règles garantissent que, peu importe comment vous additionnez, soustrayez, multipliez ou divisez ces nombres (sauf par zéro, car même en mathématiques, on ne peut pas diviser par zéro), vous obtenez toujours un autre nombre dans le même terrain de jeu.

Le lien avec la crypto : pourquoi les corps de Galois sont importants

Maintenant, vous vous demandez peut-être : "Super histoire, mais quel rapport avec la sécurité de mes mèmes de chat ?" Excellente question ! Les corps de Galois sont la base de plusieurs systèmes cryptographiques moins connus mais de plus en plus importants. Voici pourquoi ils font tant parler d'eux :

  • Efficacité : Les opérations dans les corps de Galois peuvent être incroyablement rapides et efficaces, ce qui est crucial pour le chiffrement en temps réel.
  • Résilience : Ils offrent une forte résistance contre certains types d'attaques cryptographiques.
  • Flexibilité : Les corps de Galois de différentes tailles peuvent être utilisés pour créer divers niveaux de sécurité, les rendant adaptables à différents besoins.

Les corps de Galois en action : systèmes cryptographiques réels

Voyons quelques systèmes cryptographiques qui utilisent les corps de Galois :

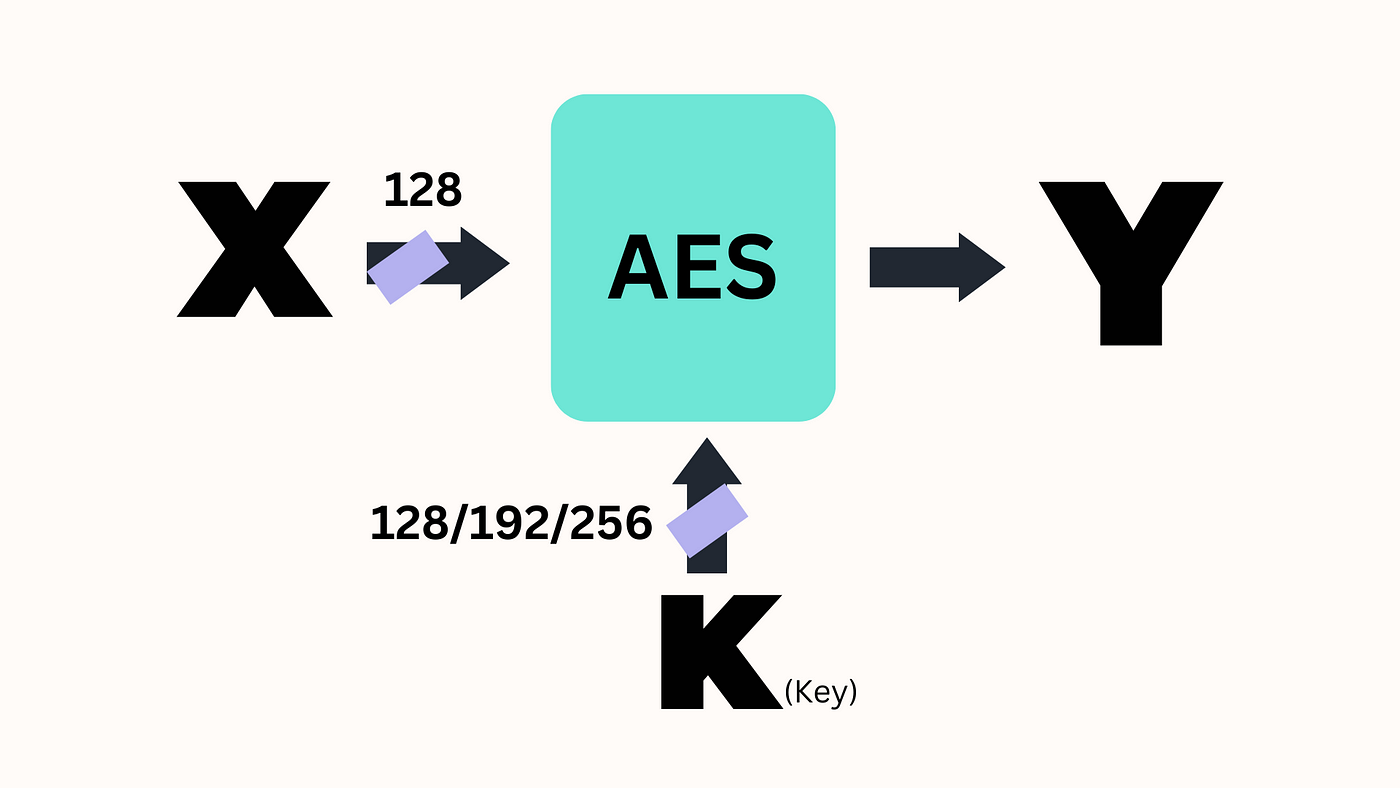
1. Advanced Encryption Standard (AES)

Oui, cet AES. Bien qu'il ne soit pas exactement "de nouvelle génération", l'AES utilise des opérations dans le corps de Galois GF(2^8) pour son étape MixColumns. Cela aide à créer la confusion et la diffusion nécessaires pour un chiffrement sécurisé.

2. Correction d'erreurs Reed-Solomon

Principalement utilisées pour la correction d'erreurs dans la transmission et le stockage de données, les codes Reed-Solomon, basés sur l'arithmétique des corps de Galois, ont également des applications en cryptographie, notamment dans les schémas de partage de secrets.

3. Cryptographie à courbes elliptiques (ECC)

L'ECC fonctionne sur des corps finis, souvent des corps de Galois. Cela permet d'avoir des tailles de clés plus petites par rapport à RSA tout en maintenant des niveaux de sécurité équivalents.

La prochaine frontière : la cryptographie post-quantique

Voici où les choses deviennent vraiment intéressantes. Alors que les ordinateurs quantiques se profilent à l'horizon, menaçant de briser bon nombre de nos méthodes de chiffrement actuelles, les cryptographes se tournent vers les corps de Galois pour développer des algorithmes résistants aux quanta.

Cryptographie basée sur les codes

Un domaine prometteur est la cryptographie basée sur les codes, qui repose fortement sur les opérations dans les corps de Galois. Le système cryptographique McEliece, par exemple, utilise des codes correcteurs d'erreurs sur des corps finis pour créer un système de chiffrement à clé publique censé être résistant aux quanta.

Voici un exemple simplifié de la façon dont un corps de Galois pourrait être utilisé en cryptographie basée sur les codes :


import galois

# Créer un corps de Galois de taille 2^8
GF = galois.GF(2**8)

# Générer un message aléatoire
message = GF.Random(10)

# Générer un vecteur d'erreur aléatoire
error = GF.Random(10)

# Simuler le codage et l'ajout d'erreur
encoded_message = message + error

# En réalité, le décodage impliquerait des algorithmes complexes
# utilisant les propriétés du corps de Galois
decoded_message = encoded_message - error

print(f"Message original : {message}")
print(f"Message décodé :  {decoded_message}")
print(f"Sont-ils égaux ?   {all(message == decoded_message)}")

Ceci est, bien sûr, un exemple très simplifié. Les vrais systèmes cryptographiques basés sur les codes impliquent des opérations beaucoup plus complexes et des tailles de corps plus grandes.

Défis et considérations

Avant de réécrire tout votre code crypto avec des corps de Galois, considérons quelques défis :

  • Complexité : Travailler avec des corps de Galois nécessite une solide compréhension de l'algèbre abstraite. Ce n'est pas pour les âmes sensibles (ou les allergiques aux maths).
  • Implémentation : L'implémentation efficace de l'arithmétique des corps de Galois peut être délicate, surtout sur du matériel non optimisé pour ces opérations.
  • Normalisation : De nombreux systèmes cryptographiques basés sur les corps de Galois sont encore en phase de recherche et n'ont pas encore été largement normalisés.

Alors, pourquoi tout ce tapage ?

Les corps de Galois sont bien plus qu'une curiosité mathématique. Ils fournissent la base d'une nouvelle génération de systèmes cryptographiques qui promettent d'être plus rapides, plus efficaces et potentiellement résistants aux quanta. Alors que nous entrons dans une ère où la sécurité des données est plus critique que jamais, ces structures mathématiques joueront probablement un rôle de plus en plus important pour protéger nos vies numériques.

Que vous soyez un passionné de cryptographie, un professionnel de la sécurité ou simplement quelqu'un qui veut paraître intelligent lors de soirées, comprendre le rôle des corps de Galois dans la cryptographie moderne vaut vraiment le détour. Qui sait ? La prochaine avancée en matière de sécurité des données pourrait bien provenir de ces champs finis aux possibilités infinies.

"L'art de faire des mathématiques consiste à trouver ce cas particulier qui contient tous les germes de la généralité." - David Hilbert

Et dans le cas de la cryptographie moderne, ce cas particulier pourrait bien être les corps de Galois. Alors, la prochaine fois que quelqu'un vous demande l'avenir du chiffrement, vous pouvez dire avec assurance : "Tout est question de Galois, de Galois, pas de problème."

Pour aller plus loin

Si vous êtes intrigué et souhaitez plonger plus profondément dans le monde des corps de Galois et leurs applications en cryptographie, voici quelques ressources pour commencer :

Rappelez-vous, dans le monde de la cryptographie, ce qui est à la pointe aujourd'hui sera obsolète demain. Restez curieux, continuez à apprendre, et qui sait ? Vous pourriez bien être celui qui découvre la prochaine grande avancée en crypto. Que le Galois soit avec vous !