Notre solution utilisera le partage de secret de Shamir pour une confiance distribuée et le chiffrement homomorphe additif pour les calculs sur des données chiffrées. À la fin, vous aurez un système backend robuste capable de détecter la fraude entre plusieurs parties sans compromettre la confidentialité des données individuelles.
Le Problème : Détection Collaborative de Fraude dans un Monde Obsédé par la Confidentialité
La détection de fraude nécessite souvent de comparer des données provenant de plusieurs sources. Mais dans notre ère soucieuse de la confidentialité, partager des données brutes est un grand non. Voici où se situe notre défi :
- Plusieurs banques doivent vérifier les activités frauduleuses dans leurs bases de clients
- Aucune des banques ne veut révéler les données de ses clients aux autres
- Nous devons trouver des schémas frauduleux communs sans exposer les enregistrements individuels
Ça ressemble à essayer de faire une omelette sans casser d'œufs, n'est-ce pas ? Eh bien, c'est exactement ce que nous permet de faire le calcul multipartite sécurisé (MPC) !
La Solution : MPC et PSI à la Rescousse
Notre approche utilisera deux techniques cryptographiques principales :
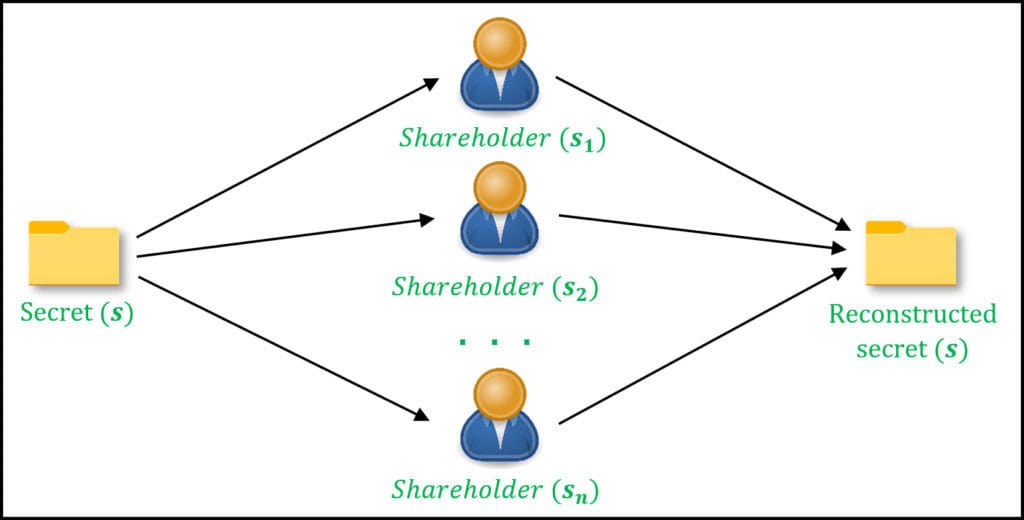
- Partage de Secret de Shamir (SSS) : Pour diviser les données sensibles en parts
- Chiffrement Homomorphe Additif (AHE) : Pour effectuer des calculs sur des données chiffrées
Nous les combinerons pour créer un protocole d'Intersection de Sets Privés, nous permettant de trouver des éléments communs entre des ensembles de données sans révéler les ensembles eux-mêmes.
Étape 1 : Mise en Place du Partage de Secret de Shamir
Tout d'abord, implémentons le partage de secret de Shamir. Cet algorithme nous permettra de diviser nos données sensibles en parts qui peuvent être distribuées entre les participants.
import random
from sympy import *
def generate_polynomial(secret, degree, prime):
coefficients = [secret] + [random.randint(0, prime-1) for _ in range(degree)]
return coefficients
def evaluate_polynomial(coefficients, x, prime):
return sum(coeff * pow(x, power, prime) for power, coeff in enumerate(coefficients)) % prime
def create_shares(secret, num_shares, threshold, prime):
coefficients = generate_polynomial(secret, threshold-1, prime)
return [(i, evaluate_polynomial(coefficients, i, prime)) for i in range(1, num_shares+1)]
# Usage
prime = 2**127 - 1 # Un nombre premier de Mersenne
secret = 1234
shares = create_shares(secret, num_shares=5, threshold=3, prime=prime)
print(shares)
Cette implémentation nous permet de diviser un secret en plusieurs parts, où tout sous-ensemble de parts (égal ou supérieur au seuil) peut reconstruire le secret, mais moins de parts ne révèlent rien sur le secret.
Étape 2 : Implémentation du Chiffrement Homomorphe Additif
Ensuite, nous allons implémenter un schéma simple de chiffrement homomorphe additif. Pour cet exemple, nous utiliserons le système de chiffrement de Paillier, qui permet des opérations d'addition sur des données chiffrées.
from phe import paillier
def generate_keypair():
return paillier.generate_paillier_keypair()
def encrypt(public_key, value):
return public_key.encrypt(value)
def decrypt(private_key, encrypted_value):
return private_key.decrypt(encrypted_value)
def add_encrypted(encrypted_a, encrypted_b):
return encrypted_a + encrypted_b
# Usage
public_key, private_key = generate_keypair()
a, b = 10, 20
encrypted_a = encrypt(public_key, a)
encrypted_b = encrypt(public_key, b)
encrypted_sum = add_encrypted(encrypted_a, encrypted_b)
decrypted_sum = decrypt(private_key, encrypted_sum)
print(f"Decrypted sum: {decrypted_sum}") # Devrait être 30
Ce schéma de chiffrement homomorphe nous permet d'effectuer des additions sur des valeurs chiffrées sans les déchiffrer d'abord.
Étape 3 : Implémentation de l'Intersection de Sets Privés
Maintenant, combinons SSS et AHE pour créer notre protocole d'Intersection de Sets Privés :
def private_set_intersection(set_a, set_b, threshold, prime):
public_key, private_key = generate_keypair()
# Créer des parts pour chaque élément de set_a
shares_a = {elem: create_shares(elem, len(set_b), threshold, prime) for elem in set_a}
# Chiffrer les parts
encrypted_shares_a = {elem: [encrypt(public_key, share[1]) for share in shares] for elem, shares in shares_a.items()}
# Simuler l'envoi de parts chiffrées à l'autre partie
# Dans un scénario réel, cela impliquerait une communication réseau
# L'autre partie évalue son ensemble par rapport aux parts reçues
intersection = set()
for elem_b in set_b:
possible_match = True
for elem_a, enc_shares in encrypted_shares_a.items():
reconstructed = sum(share * pow(elem_b, i+1, prime) for i, share in enumerate(enc_shares))
if decrypt(private_key, reconstructed) != 0:
possible_match = False
break
if possible_match:
intersection.add(elem_b)
return intersection
# Usage
set_a = {1, 2, 3, 4, 5}
set_b = {3, 4, 5, 6, 7}
threshold = 3
prime = 2**127 - 1
intersection = private_set_intersection(set_a, set_b, threshold, prime)
print(f"Intersection: {intersection}")
Cette implémentation permet à deux parties de trouver l'intersection de leurs ensembles sans révéler les ensembles eux-mêmes.
Tout Mettre Ensemble : Système de Détection de Fraude
Maintenant que nous avons nos éléments de base, créons un système simple de détection de fraude en utilisant notre Intersection de Sets Privés basée sur le MPC :
class Bank:
def __init__(self, name, suspicious_accounts):
self.name = name
self.suspicious_accounts = set(suspicious_accounts)
class FraudDetectionSystem:
def __init__(self, banks, threshold, prime):
self.banks = banks
self.threshold = threshold
self.prime = prime
def detect_common_suspicious_accounts(self):
if len(self.banks) < 2:
return set()
common_suspicious = self.banks[0].suspicious_accounts
for i in range(1, len(self.banks)):
common_suspicious = private_set_intersection(
common_suspicious,
self.banks[i].suspicious_accounts,
self.threshold,
self.prime
)
return common_suspicious
# Usage
bank_a = Bank("Bank A", [1001, 1002, 1003, 1004, 1005])
bank_b = Bank("Bank B", [1003, 1004, 1005, 1006, 1007])
bank_c = Bank("Bank C", [1005, 1006, 1007, 1008, 1009])
fraud_system = FraudDetectionSystem([bank_a, bank_b, bank_c], threshold=3, prime=2**127 - 1)
common_suspicious = fraud_system.detect_common_suspicious_accounts()
print(f"Common suspicious accounts: {common_suspicious}")
Ce système permet à plusieurs banques de détecter collaborativement des comptes potentiellement frauduleux sans révéler leurs listes individuelles de comptes suspects.
Réflexions : Implications et Considérations
Avant de vous précipiter pour implémenter cela en production, voici quelques points à considérer :
- Performance : Les protocoles MPC peuvent être intensifs en calcul. Comment optimiseriez-vous cela pour de grands ensembles de données ?
- Communication Réseau : Notre exemple suppose un calcul local. En réalité, vous devrez gérer une communication réseau sécurisée entre les parties.
- Modèle de Sécurité : Notre implémentation suppose des parties semi-honnêtes. Quels changements seraient nécessaires pour des adversaires malveillants ?
- Conformité Réglementaire : Comment cette approche s'aligne-t-elle avec les réglementations sur la protection des données comme le RGPD ou le CCPA ?
Conclusion : La Puissance du Calcul Préservant la Confidentialité
Nous n'avons fait qu'effleurer la surface de ce qui est possible avec le Calcul Multipartite Sécurisé et l'Intersection de Sets Privés. En utilisant ces techniques, nous pouvons créer des systèmes collaboratifs puissants qui respectent la confidentialité individuelle.
Rappelez-vous, dans le monde de la confidentialité des données, nous ne faisons pas que coder – nous construisons la confiance. Donc, la prochaine fois que quelqu'un vous dira que la confidentialité et l'utilité des données sont mutuellement exclusives, vous pourrez dire avec confiance : "Tenez ma bière chiffrée homomorphiquement !"
Bon codage, et que vos calculs soient toujours sécurisés !
"En Dieu nous avons confiance. Tous les autres doivent apporter des données." - Et maintenant, grâce au MPC, ils peuvent apporter des données sans réellement les apporter !